Přinášíme další krátký pravdivý příběh Milana Hejného o tom, jak se děti učí. Tentokrát jde o ukázku toho, jak se děti samy pod správným vedením dopracují nejen k tomu, kolik dvojic lze sestavit z n prvků, ale také že tato znalost bude propojena na životní zkušenosti žáka, a tedy dobře sémanticky ukotvená (viz. Příběh #1). Nejzajímavější ovšem na tomto příběhu je, že děti už v sedmé třídě alespoň intuitivně pochopí pojem izomorfismus.
Z příběhu je opět vidět, že se mýlí ti, co si myslí, že Hejného metoda je jen pár nahodilých nápadů.
Šest izomorfních úloh
(podle textu Milana Hejného Poznávací proces (v matematice))
V sedmém ročníku jsem chtěl žáky dovést k objevu vztahu:
[latex s=2]\binom{n}{2} = \frac{n\cdot(n-1)}{2}[/latex]
(Pro ty, co to už zapomněli: výraz vlevo se čte ‚n nad dvěma‘ a udává, kolik různých dvojic lze sestavit z n prvků.) Zvolil jsem strategii postupných objevů pro n = 5, 6, … Nejprve jsem ve třech po sobě jdoucích dnech (pondělí, úterý, středa), vždy ke konci hodiny, dal třídě postupně následující tři úlohy.
Úloha #1
Kolik různých přímek je tvořeno vrcholy pravidelného pětiúhelníku?
Úloha #2
Zjistěte, kolika způsoby se dá přečíst slovo KAMILA v přiložené tabulce. Začínáme nahoře vlevo a končíme dole vpravo. Chodíme jen vpravo nebo dolů.

Úloha #3
Ze dvou červených a tří modrých krychlí stavím pětipodlažní věže. Kolik různých věží mohu postavit?
Očekával jsem, že když žáci zjistí, že výsledek je pokaždé 10, tak také odhalí, že úlohy jsou izomorfní. (Tedy, že matematický model úloh je shodný, i když úlohy na první pohled vypadají naprosto odlišně.) Žáci úlohy bez problému vyřešili, ale izomorfismus neodhalili. Proto jsem ve čtvrtek hned na začátek hodiny připomněl tři předchozí úlohy a dal úlohu další:
Úloha #4
Na turnaji ve fotbale bylo přihlášeno pět mužstev. Hrálo se systémem každý s každým jeden zápas. Kolik proběhlo zápasů?
Již po chvíli několik žáků ukázalo, že úlohy #1 a #4 jsou izomorfní. Každý vrchol pětiúhelníku je jedno mužstvo a přímka spojující dva vrcholy je zápas mezi příslušnými mužstvy. Několik žáků vyslovilo názor, že i ty další budou stejné.
Kristýna na konci hodiny ukázala, že i úlohy #2 a #3 jsou stejné. Řekla „když jdu po té Kamile například vpravo, vpravo, dole, vpravo, dole (cestu zakresluje do tabulky), tak to je věž, která má (dívka na tabuli kreslí věž zdola nahoru) modrou krychli, modrou, červenou, modrou, červenou krychli“.
Po přestávce, když jsem již odcházel ze školy, doběhl Arpád a ukázal mi, jak souvisejí věže a fotbalový turnaj. Očísloval krychle u věže i mužstva čísly 1, 2, 3, 4 a 5 a řekl, že když jsou ve věži třeba krychle 2. a 5. červené, tak to značí zápas mezi mužstvy 2 a 5. Svým objevem byl nadšen a vykládal jej kamarádům.
Následující hodinu již snad polovina třídy věděla, že všechny čtyři úlohy jsou stejné (izomorfní), ale nevím, zda byl ve třídě žák, který by dokázal ihned najít přímý vztah mezi kterýmikoli dvěma z daných úloh. Ke konci hodiny jsem dal žákům ještě dvě další úlohy.
Úloha #5
Fotbalový zápas skončil výsledkem 3:2. Kolik různých průběhů mohl mít?
Úloha #6
Kolika způsoby je možné rozmístit 3 kuličky do tří misek: A, B, C?
Kristýna skoro ihned propojila úlohu #5 s úlohou #2. Ukázala princip propojení: „když dají gól domácí, jdu ve jménu KAMILA doprava, když dají gól hosté, jdu dolů“.
V úterý již Ivan třídě vyložil, že všechny ty úlohy, kromě poslední, jsou na jedno brdo. Stačí si ty věci očíslovat 1, 2, 3, 4, 5, pak vždy dvě z těch čísel zvolit. Tímto uchopením všech úloh pomocí jediného značení hoši objevili kombinatorický pojem, který matematici zapisují [latex s=2]\binom{5}{2}[/latex] a nazývají „pět nad dvěma“.
Na žádost třídy Arpád na tabuli ukázal, jak očíslování udělá v jednotlivých úlohách i to, jaký prvek pak odpovídá dvojici například 2 a 5:
- u pětiúhelníku očísluji vrcholy a přímkou spojím body 2 a 5
- u KAMILy očísluji pohyby; druhý a pátý půjdu dolů, u ostatních půjdu vpravo; tedy jdu dolů u písmen A a L.
- v turnaji očísluji mužstva; spolu hrají družstva 2 a 5
- u věže očísluji krychle třeba odspodu; červené jsou druhá a pátá krychle
- ve fotbalovém zápasu očísluji góly; hosté dali druhý a pátý gól.
Nakonec Ivan dodal, že nejlépe to všechno vidět na tom pětiúhelníku. O úloze #6 prohlásil, že i když výsledek vychází 10, tato úloha k našim nepatří.
Po týdnu jsem se k úlohám vrátil s výzvou, abychom v nich počet prvků zvýšili z pěti na šest. Upřesnil jsem, že v úloze #2 to bude obdélník 4 2 se jménem MARTINA, v úloze #3 budu mít 2 červené a 4 modré krychle, v úloze #5 bude výsledek 4:2 a v úloze #6 do tří misek budeme vkládat 4 kuličky.
Řešení všech úloh bylo nalezeno velice rychle, výsledek byl 15. Pouze do nové úlohy #6 se nikomu nechtělo. Nakonec se do toho pustily dvě dívky, které všechny případy rozkreslovaly. Dospěly též k výsledku 15.
Diskuze třídy trvala sotva 10 minut a byla přerušena Kristýnou, která řekla, že když v úloze #1 místo pěti-, nebo šesti-úhelníku vezmeme třeba 10úhelník, tak přímek bude 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45. Na tabuli ukázala, že začne s vrcholem 10 a ten spojí se zbývajícími devíti. Pak vrchol 9 spojí s vrcholy od 1 do 8. Poté vrchol 8 s vrcholy od 1 do 7. Tak půjde až do konce.
Během tohoto vysvětlování přišla k tabuli Hela a beze slova nakreslila tabulku
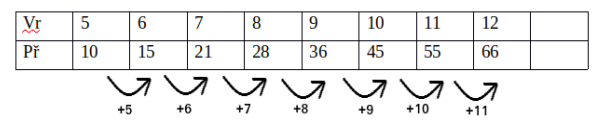
Když Kristýna skončila svůj výklad, Hela vysvětlila že „Vr“ je počet vrcholů a „Př“ počet přímek. Že se postupně přidává 5, pak 6, pak 7 a z tabulky vidět jak to půjde dále.
Ivan řekl, že to je dobře, ale dá se to počítat tak, že „z každého vrcholu toho 10úhelníku vedu 9 přímek; to jsem každou přímku počítal dvakrát; tak vezmu z nich jen polovinu. Takže to bude“ a hoch napsal na tabuli (10 x 9):2. Třída souhlasila. Na můj dotaz, jak by to bylo pro n-úhelník, Kritýna řekla, že se to sečtou čísla od n až do jedné. Ivan řekl, že stejně, jen místo 10 by tam bylo n. Napsal jsem tedy (n x 9):2. Třída nesouhlasila, že i těch 9 je třeba změnit. Chvíli to trvalo, než se třída dobrala k zápisu (n x m):2, m = n – 1. Pak ale někdo napsal:
[latex s=2]\frac{n\cdot(n-1)}{2}[/latex]
Ivan řekl „jo, takhle je to lepší“. Nakonec jsem řekl, že matematici to zapisují [latex s=2]\binom{n}{2}[/latex] a čtou „n nad dvěma“. Na to, proč je i úloha #6 izomorfní s ostatními přišli Kristýna s Ivanem až v osmém ročníku.
Přijdete na to vy?
Příběhy uveřejňujeme s laskavým svolením profesora Milana Hejného, který je zaznamenal během své dlouhé učitelské praxe a Ondřeje Šteffla, který je přichystal k publikování.
DOPORUČENÉ ČLÁNKY
21. 08. 2022 Bára Procházková Pět věcí, které budou v novém školním roce jinak
28. 02. 2023 Lucie Rybová Život celé rodiny se zúžil na domácí úkoly, podle právníků jsou navíc nezákonné



Jestli to dobře chápu, tak těm dětem nikdo neřekl, že úloha 6 je nemlich totéž jako ostatní úlohy? Čekal bych, že to učitel na konci bloku shrne a vysvětlí, ne že bude čekat, až na to žáci přijdou sami o rok později. Rozhodně myslím, že je správné, když žáci vše co se v matematice učí dokonale pochopí (a že co nepochopí, nemá smysl učit ani zkoušet), ale přeci jenom bych to těm méně hloubavým (nebo těm, kteří si jenom něčeho nevšimli) raději nakonec ukázal 🙂 Po matematicku řečeno bych jim předložil důkaz izomorfismu obou úloh. Kdyby takhle učitel například čekal, až sám od sebe pochopím, jak se násobí kvaterniony, tak bych seděl v posluchárně ještě teď, zatímco bystřejší Hamilton na to přišel už za několik málo let. Začínám si myslet, že zatímco premisy Hejného metody jsou ok, praktické provedení se jeví až moc „alternativní“ 🙂
Při popsaných aktivitách pracují Ivan, Kristýna, Arpád a Hela. Každý z nich učiní nějaký dílčí objev, k tomu, co bylo cílem, nedojde v té chvíli ani jeden z nich (dva o rok později, fajn). Co dělá v té době zbytek třídy? Jaký přínos mají hodiny pro ně? A co děti, které v některých z hodin chyběly a nemohly tedy ani sledovat myšlenkové pochody spolužáků? Nějaké vysvětlení a shrnutí v učebnici zřejmě čekat nemůžou. Pokud by třída dostala podobnou úlohu v devítce, projeví se nějak, že tohle všecko hledání proběhlo, nebo Kristýna s Ivanem projdou znova celou cestu a ostatní se o to budou maximálně pokoušet, přičemž se někde ztratí?
Oba předchozí příspěvky vycházejí z chybného předpokladu, že nutnou podmínkou pro pochopení izomorfismu je vyřešení všech úloh na dané téma. Ten, kdo pochopil rozklad na prvočinitele, musí být schopen rozložit čísla 30 nebo 154, ale pokud nezvládne rozložit 41 824 268 143 841 759, neplyne z toho, že se nic nenaučil.
Spojit Úlohu 6 s ostatními mi trvalo přes hodinu (povedlo se mi to až přes #2). Nepotřeboval jsem další rok výuky, jen nápad co vlastně očíslovat od jedné do pěti (šesti/n), když evidentně nelze číslovat kuličky ani misky.
V klasické učebnici by #6 byla příklad s hvězdičkou a nikoho by kvůli němu nenapadlo tvrdit, že průměrný žák neumí, nebo se mu učitel špatně věnoval.
Jasně, to chápu. Jenom to bývalo tak, že když se příklad začal veřejně řešit (u tabule), tak se také veřejně dotáhl do konce. Ale třeba to tak bylo, jenom jsem to z článku pochopil jinak 🙂
Dobře, rozumím. Cílem souboru úloh tedy je, aby žáci pochopili izomorfismus. U kolika z nich byl cíl splněn? Co znamená formulace, že „několik žáků ukázalo“? Byli to dva, nebo patnáct? „Snad již polovina třídy věděla, že úlohy jsou stejné.“ – jak učitel ví, že to věděli? To v článku není. A přišli si na to (tak, jak HM hlásá, že by to mělo být), nebo to prostě uvěřili spolužákovi, o němž vědí, že mu matika jde? A znovu – co ti, kteří chyběli a budou se ptát, co se mají doučit?
Ty otázky na měření plnění cíle jsou legitimní, kdyby to byl scientific paper, asi by to v článku bylo. K těm se klidně připojuju, ale to by pak po pointě místo krátkého call-to-action pro čtenáře končil článek dlouhou rekapitulací té hodiny v osmé třídě, kde to učitel znovu vytáhl.
Ohledně toho, co se mají žáci doučit – no v ideálním případě si o tom budou muset se spolužáky popovídat (jako se to dělo v hodině). Asi to není vůči nevinnému absentérovi spravedlivé, ale kritérium: „Jak snadno doženu zameškanou hodinu z učebnice?“ se mi zdá být poměrně spolehlivým indikátorem kvality metody v opačném směru (snadné = nekvalitní).
Pokud mě jako učitele někdo přesvědčuje k tomu, abych použila určitou metodu, ptám se, k jakému cíli mám touto metodou dojít a jak poznám, že se to opravdu povedlo. Pokud mi na to není schopný odpovědět, sory, ale pak to není metoda, ale experiment – a děti nejsou pokusní králíci.
Chybějící dítě si může popovídat s jakýmkoli spolužákem? Nebo k tomu potřebuje Kristýnu s Ivanem? Pokud učit kvalitně znamená učit složitě, velmi ráda zůstanu nekvalitním učitelem 🙂
Mno. Nevím, jestli je HM souborem nahodilých nápadů. Toto tvrzení, které je v článku podsouváno zřejmě kritikům HM, jsem tady (pokud se dobře pamatuji), nikdy nezaregistroval v žádném rozumném příspěvku. Buďme slušní a nazvěme to třeba otevřeně sugestivní poznámkou.
Upřímně ale doufám, že to, jak jsou položené ty úlohy, které jsou v článku popsané, se ztratilo někde v překladu, a že takto pan profesor ony úlohy ve skutečnosti nepokládá. Proč? Třeba proto, že bez jakékoliv početní námahy je správné řešení první úlohy vždy NULA, bez ohledu na zvolený geometrický obrazec.
Ivan, Hela, Kristýna a Arpád vynikající, na 7. třídu tedy rozhodně klobouk dolů ! Jen se obávám, že zbytek třídy nestíhá a jen kouká. Určitě nezavrhuji využívání Hejného prvků ve výuce, u našich dětí jsme je také doma s radostí dobrovolně používali, učebnice jsou skvělé… Jen si stále myslím, že obecně by bylo mnohem prospěšnější než Hejného metoda jedna učitelka/na 30 žáků, raději cokoliv jedna učitelka/na 15 žáků, kde je šance na individuální přístup. Mnoho dětí ačkoliv intelektuálně schopných je třeba pomalejších a chvilku jim trvá, než pochopí problém do hloubky, ne každému také sedí určitý styl výuky apod. Osobně panu Hejnému a jeho následovníkům velmi fandím, jsou úžasní a zapálení. Jen jsem se také setkala s rodiči s velmi negativním názorem poté, co Hejného metodou jejich děti prošly, sama tedy upřímně nevím, nechce se mi vybírat jedna ze stran. Nejlepší by bylo zavedení alespoň některých prvků Hejného metody do standartní výuky plošně, ale tomu se zase brání strana Hejného metody, jelikož to pak údajně není ono (nemá daný efekt). No nevím, syn měl tři roky úžasnou učitelku, která byla na mnoha školeních Hejného metody a ačkoliv se Hejného metodou na dané škole neučí, tak úspěšně aplikovala do standartní výuky právě mnoho prvků z ní. Naprosté nadšení rodičů i dětí…
Díky bohu se mě ani mých děti , Hejného matematika netýkala. Jedno z děti je učitel M pro základní i střední školu. Na tuto metodu mám zcela jasný názor. Za mne je to plkání o ničem (panu Hejnemu se tímto omlouvám s ohledem na mou vrozenou úctu ke starším lidem) Opravdu bych asi nedala, kdyby mé děti „hledaly“ řešení. Mé dětí tu matematiku prostě umí, on by totiž na gymnáziu či na vysoké škole nikdo nečekal až na řešení pokus omyl přijde.
Na druhou stranu je umět a „umět“. V podstatě každý je schopen se naučit vyčíslit výraz n nad k, aniž by věděl jak se k němu došlo a co všechno se tím dá vypočítat. Ale jsou učitelé kterým to takhle stačí a tvrdí o takovém žákovi, že to „umí“. A já si pořád myslím, že Hejného metoda má zabránit žákům i učitelům aby to takhle dopadlo.
Tak článek je o základní škole. Tak nějak si myslím, že učivo základní školy by měl zvládnout každý a stejně tak by mu měl rozumět. Nebo máte snad dojem, že zvládnout matematiku ZŠ zvládne jen einstein? Nebo snad chci moc, když očekávám znalost zlomků, měrných jednotek, procent či rovnic? To je věc, která je potřebná pro běžný život. Třeba proto, aby se vám nestalo, že když si necháte postavit garáž, tak vám zedník objedná cihel jak na mrakodrap. Protože neumí spočítat množství (objem, obsah). Prostě idiot s kvalitním wifi připojením není kvalifikace. A ani Hejného natematikou to neokecáte.
Umět mechanicky vypočítat, i když člověk nerozumí tomu proč zrovna tímto způsobem, často prostě postačí.
Shrnula jste to výstižně, ale to je právě ta věc se kterou nesouhlasím. Aspoň co jsem kdy viděl, tak když člověk vůbec netuší proč se něco počítá zrovna takhle, tak to nakonec stejně není schopen správně použít. Před nějakou dobou jsem tu uváděl příklad studenta, který neuměl z řezné rychlosti spočítat otáčky soustruhu. Myslím, že to by měl spočítat každý, kdo někdy v životě viděl soustruh a odhadne co asi může znamenat „řezná rychlost“. Ale on byl zrovna typ, který se nadřel všechny vzorečky a vzorová řešení úloh nazpaměť (takže udělal přijímačky atd.), ale tenhle vzoreček mezi nimi zrovna nebyl, tak nevěděl kudy kam 🙂 V ideálním školství by ho ve škole pérovali tak dlouho, dokud by to nepochopil, i kdyby to znamenalo, že se nestihne „naučit“ logaritmy a rovnice o dvou neznámých 🙂
Super, mám ale za to, že 7. ročník je ročníkem, ve kterém se definují celá a zejména racionální čísla, tedy zlomky. To jest úpravy zlomků, součet, rozdíl, násobení, dělení … To vše se dělá pro to, aby v 8. ročníku přišli na řadu mocniny, odmocniny a výrazy s proměnnou … To mi tedy jako matikáři přijde stěžejní pro další působení na jakékoliv škole … Je tedy moc hezké, že děti dokáží „intuitivně“ odvodit kombinační čísla, ale já se spíš ptám, co ten základní matematický aparát, na které se potom staví a také na kterém končí drtivá většina studentů po příchodu na střední školu …
A ještě jedna vsuvka … pravděpodobnost se na základní škole prakticky nevyučuje, protože je k ní právě potřeba ten matematický aparát (faktoriály, apod.). Ano … kolik dvojic musím sestavit, aby hrál každý s každým, dám pouze s násobením. Tedy je krásné, že děti na něco přišly, ale co to ostatní, co mají umět. Ovládají ten základ na takové úrovni, aby mohli jít dál? Nebo sice dohnali „hloupou Kristýnku a Ivánka“, ale tím to tak skončilo, protože ti dva mají ten aparát a nyní uvidí pan Hejný, jak se před ním zaprášilo.
A ještě jedna otázka, která by mě opravdu zajímala.
Kdo je autor textu a jaké má vzdělání? Jaká je jeho pedagogická zkušenost, kde učil … To tu jaksi chybí …
Ale no tak, Martine, se zlomky už se přece děti vypořádaly ve čtvrté třídě, když Ivan přišel na to, že myš má stejnou sílu jako čtvrtka psa 🙂 🙂 🙂
Ale vážně. V letošním školním roce u nás na škole došly do devítky první děti, které byly vedené Hejného metodou na druhém stupni. V pololetí odešla paní učitelka na mateřskou a děti dostaly učitelku učící klasicky. První cesta vedla do papírnictví koupit pravítko – děti ho od konce pětky neměly v ruce. Na střední školy se dostali vesměs ti, kteří paralelně se školní výukou chodili na doučování.
Hejného metoda nevyhovuje všem dětem. Zvládají ji dobře děti s logickým myšlením. Ostatní se jen vezou. Zpočátku, tak do třetí třídy, je to takové hraní, které baví skoro všechny děti. Od čtvrté třídy začíná přituhovat a tak půlka dětí ve třídě přestává chápat, co se po nich vlastně chce. Rodiče tomu také nerozumí, tak nastupuje doučování. A to si myslím, není zrovna to, co by se panu Hejnému líbilo. Naštěstí již hodně škol na to přišlo, a začalo používat Hejného metodu jen jako doplněk ke klasické matematice. Rodiče po počáteční euforii s „novou a zábavnou“ matematikou, již mají také dost informací od starších, takže pokud si mohou vybrat, tak spíš volí klasickou výuku matematiky.
„Zvládají ji dobře děti s logickým myšlením.“
Tím myslíte, že HM vyžaduje od žáků schopnost logicky myslet, nebo že žáci, schopní logicky myslet, se dokážou přenést přes věci, které by v klasické matice nezažili? 😀
Nemusíte odpovídat, to byla vlastně řečnická otázka. Chtěl jsem tím naznačit, že matematika na zš má přece rozvoj logického myšlení především stimulovat, a ne vyžadovat. 😉
Zdravím, souhlasím s názorem, že MT podle prof. Hejného není pro všechny. Syn má ve škole tuto metodu od první třídy, momentálně půjde do 7. třídy a mohu říci, že jeho znalosti matematiky jsou slabé. Syn má poruchu soustředění a pozornosti, pozornost udrží cca 5 – 10 minut, potom je mimo. V 6. třídě dostal z MT na vysvědčení čtyřku. Názor učitelky: „hold MT nebude jeho silná stránka“. Ano, na MT nebude génius, ale hlupák není. Bohužel ho brzdí ADHD. Takže jsem donucena mu zařídit pro tento školní rok doučování a teď otázka, doučování na normální MT nebo na MT dle prof. Hejného? V 7. třídě pojedou ještě metodou prof. Hejného a v 8. třídě se budou učit MT dle staré metody z důvodu přijímaček na střední školy. Takže dle mého názoru jeden velký guláš a chaos. Myslím si, že MT dle prof. Hejného není špatná, ale je to metoda pro chytré děti, a tento můj názor mi potvrdilo už i pár učitelů. A samozřejmě dost důležitý je při této metodě kvalitní učitel/ka.
Jestli je to doučování kvůli přijímačkám, tak určitě „klasiku“. U přijímaček je dost jedno, jestli tomu žáci rozumějí, tam jde o to, aby to uměli. Porozumění je už jen nepovinný bonus 🙂 Osobně si sice myslím, že když tomu rozumím, naučím se to mnohem snáz, ale ověřil jsem si, že to tak nefunguje u každého.
Poslední věta je poněkud nemístný vtip. Nebo to skutečně myslíte vážně?
Jakou kvalitu má asi výuka, kde je nutné, aby žáci měli ještě doučování. Ať už je systém výuky jakýkoliv, tak takovýto názor je skutečně nebezpečný.
Na jaké škole to prosím takto funguje, ať se ji mohou všichni co si počtou vyhnout?
Toť otázka, jestli je to chyba, jak velká a čí vlastně. Sám to vidím tak, že se postupně naplňuje snaha státu o převedení školství do soukromých rukou. Zatím postupně, že každý „kdo to chce někam dotáhnout“ musí mít soukromého učitele paralelně ke státní škole, což je bohužel ta nejkomplikovanější varianta. Daleko lepší by bylo mít možnost odhlásit dítě z matematiky a učit tento předmět doma (tj. zpravidla pomocí najatého soukromého učitele či soukromé školy). Druhá věc která mě napadá je, že dotyčné střední školy zajímají u zkoušek jen ty nejformálnější výsledky výuky matematiky a už si neověřují, jestli to ty děti třeba neumějí „trochu jinak“, třeba i z hlediska další výuky matematiky lépe.
Také mě zaujalo, k čemu se asi učí kombinační čísla na základní škole. Řekl bych, že to poněkud vybočuje z hejného principu učit se to, co využijí, a na tom, co znají. A kombinatorika je učivo střední školy, takže pokud jsou v sedmé třídě, budou to potřebovat nejdříve za dva roky, ale většina z nich se to ani nikdy učit nebude, protože tato matematika se, pokud vím, neučí jen tak na každém učilišti.
My jsme měli kombinatoriku (základy ovšem) už na základce. A imho je to důležitá životní dovednost, jak chcete hrát třeba poker a nevědět jakou máte šanci třeba na full house. To pak prosázíte kalhoty a nic z toho…
Za moji maličkost: své dítě bych do školy, kde se vyučuje podle metody pana Hejného, nedal ani náhodou, i kdyby to bylo podmíněno dojížděním. Tuto metodu jsem ochoten tolerovat nanejvýš jako doplněk ke klasické výuce.
Až do dnes jsem nevěděla o izoformismu vůbec nic. (nebo jsem to zapomněla)
Za sebe musím říct, že mi asi stačí umět násobit, dělit, sčítat, odčítat a pochopení procent, zlomků. Na střední zemědělské škole jsem měla matematiku jen 2 roky.(sinus, kosinus, tangens, kotangens…to jsem ještě pobrala, ale už si to nevybavím) Není nic proti ničemu, když někdo umí a chápe i „složitější matematiku“, ovšem velké části lidí, podle mně, stačí pevné základy a ty když nejsou, tak je to průšvih.
Když tyto děti dospějí a bude jim 40 let, bude mezi nimi a dospělými bez HM nějaký podstatný rozdíl? Budou lepšími pracovníky, rodiči, řidiči…budou šťastnějšími? Může být HM výhybkou v životě člověka, nebo je to pořád jen matematika jinak?
No, řekl bych, že je to hlavně matematika jinak. Učit se („intuitivně“) kombinační čísla roky předtím, než je možná použijí na střední škole, a to ještě ne zdaleka všichni, se na běžné škole nedělá. Zajímalo by mě, proč ve článku není Hejného vysvětlení, proč dělá tuto zdánlivě nesmyslnou věc, pokud jsem je teda nepřehlédl.
Václave, intuitivní pochopení izoformismu má být na tom příběhu to nejzajímavější.:)
Znalost, kolik dvojic lze sestavit z n prvků, bude propojena na životní zkušenosti žáka, a tedy dobře sémanticky ukotvená.
Ovšem k čemu je to, v 7. třídě, dobré, mi uniká.
Markéto, možná jsem moc přízemní pragmatik, který potřebuje jako nutnou, nikoliv však postačující podmínku, vidět smysl. 😀 I když si myslím, že často vidím (ne)smysl i tam, kde ho většina nevidí (což není vždy kompliment), ve studiu kombinačních počtů a izomorfismu před sš jej nevidím a čekám, že mě někdo vyvede z omylu. Můj předpoklad je takový, že kdyby se od běžného třináctiletého dítěte dalo čekat, že pracuje třeba na nějaké vědecké práci, nebo na znalostně náročné pozici u rodičů ve firmě (že by na to byla potřeba obezlička kvůli zákazu dětské práce, to prosím pro teď nerozebírejme), nebo cokoliv jiného, kde by potřebovalo třeba statistiku, která je kombinatoriky plná, tak bych neřekl ani popel a podporoval to všema deseti, ale myslím, že to se dá čekat individuálně u výjimečně nadaných a/nebo houfně nejdříve u středoškoláků, kteří si podle toho také vybírají školy, kde je to naučí jako součást učiva. Takže ani z tohoto důvodu podle mě není kombinatorika na zš potřeba.
Můj osobní závěr je tedy takový, že pokud se tím Hejný skutečně může pochlubit (což nevylučuji, ale ani tomu nejsem moc nakloněn), chlubí se něčím, co nemá praktickou hodnotu pro žáky. Z toho IMHO čouhá jen vylepšení ega, image a posléze příjmů pana Hejného.
P.S.: omlouvám se, možná s tím poukazováním na příjmovou stránku věci už otravuju, ale dle mého názoru nejde dost podcenit vliv toho, že pan Hejný zde nevystupuje pouze jako kantor, ale také jako podnikatel, kterému EDUin dělá ohromnou reklamu… to ta má pragmatická stránka 🙂
Já proti pragmatismu nic nenamítám. 🙂
Smysl? Co třeba proto, aby děti zažily radost ze samostatného poznávání matematiky, aby si užily potěšení z odhalování jejích zákonitostí? Aby zjistily, že pokud je to baví, mohou bádat a hledat souvislosti samy a nemusí čekat, až na nějaký jev narazí v osnovách? Nebo naopak, aby si jiné děti ujasnily, že tohleto jim nic neříká, že matematika asi není jejich parketa, a že bude vhodnější zaměřit se na zlomky, procenta a trojčlenku, které uplatní ve svém občanském životě, a jinak se raději soustředit na jiné obory?
Nevím proč tomu musí říkat zrovna izomorfizmus 🙂 Je to sice pravda, ale je to už taková matematická hantýrka. Kdyby hezky česky řekl, že vede žáky k hledání souvislostí mezi zdánlivě různými úlohami, udělá myslím líp 🙂
Naučit se hledat a vidět souvislosti i tam, kde na první pohled vidět nejsou, je užitečné pro život jako takový. A ano, hezky česky by to bylo lepší.
Ovšem zřejmě už by to tak nevyznělo.:)